Visualising Array Sections

Consider the declaration

    REAL, DIMENSION(1:6,1:8) :: P

 
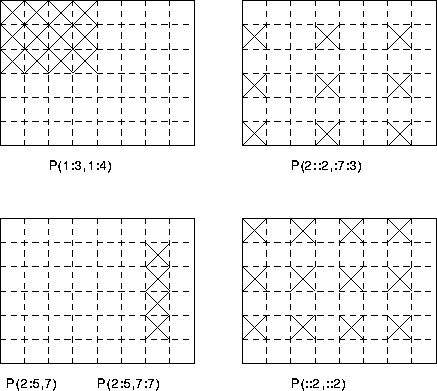
Figure 4: Visualisation of Array Sections

The sections:

• P(1:3,1:4) is a 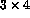section; the missing stride implies a value of 1,
• P(2::2,:7:3) is a 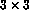section; the missing upper bound (in the first dimension) is the upper bound as declared, (6), the missing lower bound is the lower bound as declared, (1).
• P(2:5,7) is a 1D array with 4 elements; P(2:5,7:7) is a 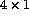2D array,
• P(::2,::2) is a 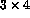section. Both upper and lower bounds are missing so the values are taken to be the bounds as declared, this is equivalent to P(1:6:2,1:8:2).

Conformance:

• P(1:3,1:4) = P(::2,::2) is a valid assignment; both LHS and RHS are 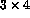sections.
• P(1:3,1:4) = 1.0 is a valid assignment; a scalar on the RHS conforms to any array on the LHS of an assignment.
• P(2::2,:7:3) = P(1:3,1:4) is not a valid assignment; an attempt is made to equate a 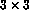section with a 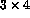section, the array sections do not conform.
• P(2::2,:7:3) = P(2:5,7) is not a valid assignment; an attempt is made to equate a 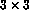section with a 4 element 1D array.

It is important to recognise the difference between an n element 1D array and a 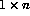2D array:

• P(2:5,7) is a 1D section -- the scalar in the second dimension `collapses' the dimension.
• P(2:5,7:7) is a 2D section -- the second dimension is specified with a section (a range) not a scalar so the resultant sub-object is still two dimensional.

Now try this question